参考:数据结构:八大数据结构分类、(单向、单向循环、双向、双向循环)链表学习总结
数据结构是为算法服务的,算法要作用在特定的数据结构之上
想要学习数据结构与算法,首先要掌握一个数据结构与算法中最重要的概念-复杂度分析

10 个常用数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie树
10个常用算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
数组
- 介绍:
- 可以在内存中连续分配的数据结构
- 元素通过下标进行访问
- 优点:
- 按照索引查询速度快
- 按照索引遍历方便
- 缺点:
- 元素删除、新增操作慢,需要移动其他元素
- 只能存储单一类型的元素
- 容量在初始化时确定下来,无法扩容
- 适用场景:
- 查询频繁,删除、新增操作少,对存储空间要求不大
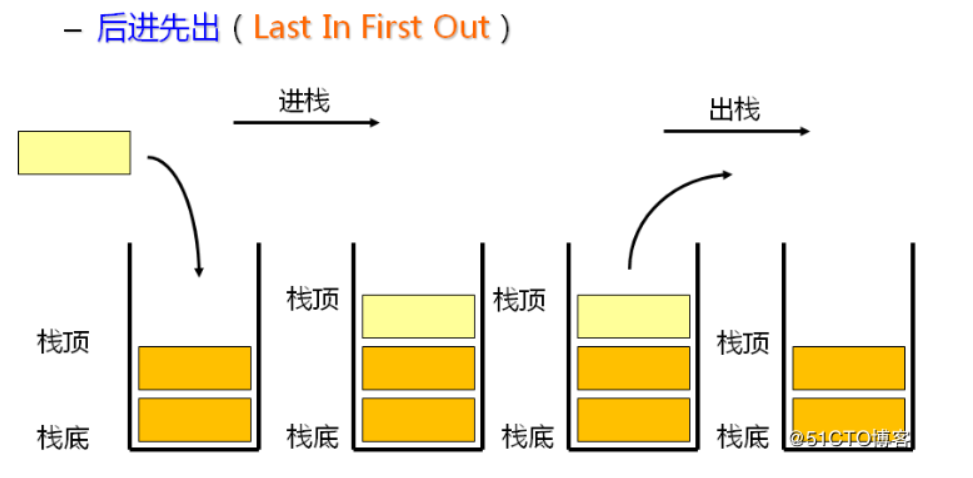
栈
- 介绍:
- 一种特殊的线性表,只能在线性表的一端操作
- 栈顶允许操作,栈底不能操作
- 特点先进后出
- 栈顶放入元素成为入栈(PUSH),取出元素称为出栈(POP)
优点:
缺点:
适用场景:
- 递归等场景
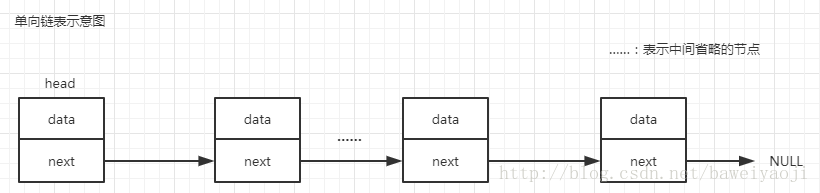
链表
- 介绍:
- 物理存储单元上非连续、非顺序的存储结构
- 数据元素的逻辑顺序是通过链表指针实现的
- 每个元素包含两个节点:一个存储元素的数据域,一个指向下一个节点的指针域
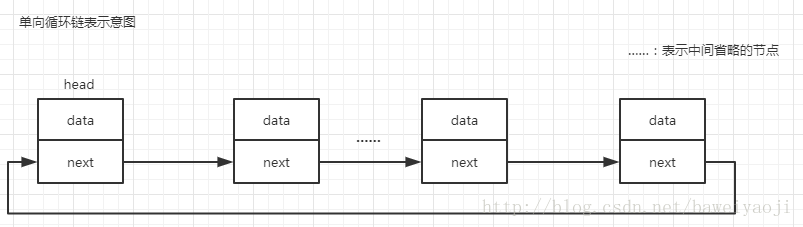
- 根据指针的指向,可以分为:单链表、双向链表、循环链表
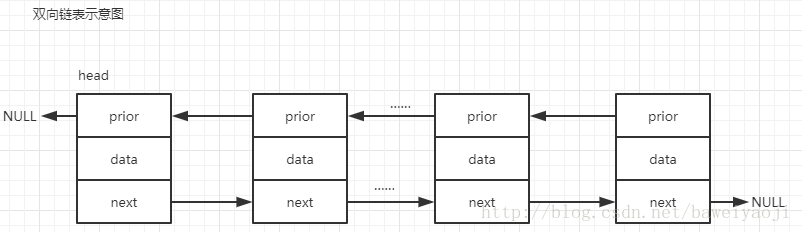
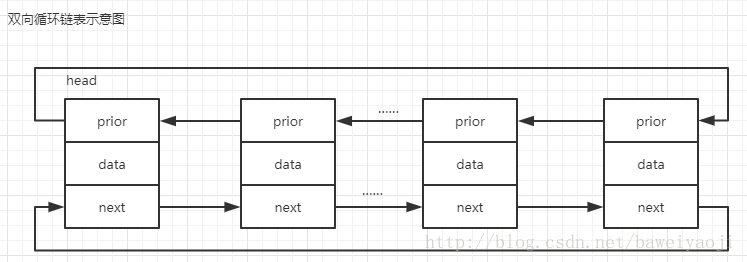
- 优点:
- 不需要初始化,可以随意添加、删除元素
- 添加、删除只需要修改改变前后两个节点的指针域指向地址即可,所有添加、删除操作速度快
- 缺点:
- 因含有指针域,所以占用空间大
- 查询元素比较耗时,需要遍历整个链表
- 适用场景:
- 数据量小,但是需要频繁添加、删除的场景
队列
- 介绍:
- 一种线性表
- 可以在一端添加元素,另一端取出元素,即先进先出
优点:
缺点:
适用场景:
- 阻塞队列
图
- 介绍:
图是由结点的有穷集合V和边的集合E组成。其中,为了与树形结构加以区别,在图结构中常常将结点称为顶点,边是顶点的有序偶对,若两个顶点之间存在一条边,就表示这两个顶点具有相邻关系。
按照顶点指向的方向可分为无向图和有向图: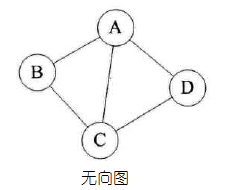
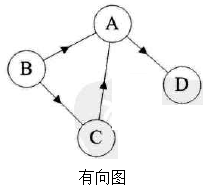
图是一种比较复杂的数据结构,在存储数据上有着比较复杂和高效的算法,分别有邻接矩阵 、邻接表、十字链表、邻接多重表、边集数组等存储结构
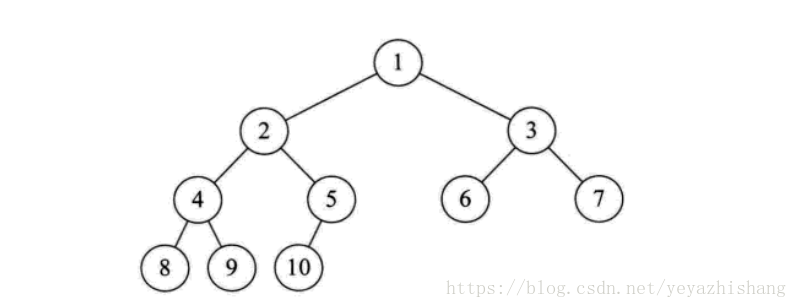
树
- 介绍:
- 由n(n>=1)个元素组成的具有层次关系的集合
- 每个节点有零或者多个子节点
- 没有父节点的节点为根节点
- 每一个非根节点有且只有一个根节点
- 除了根节点,每个子节点可以分为多个不相交的子树
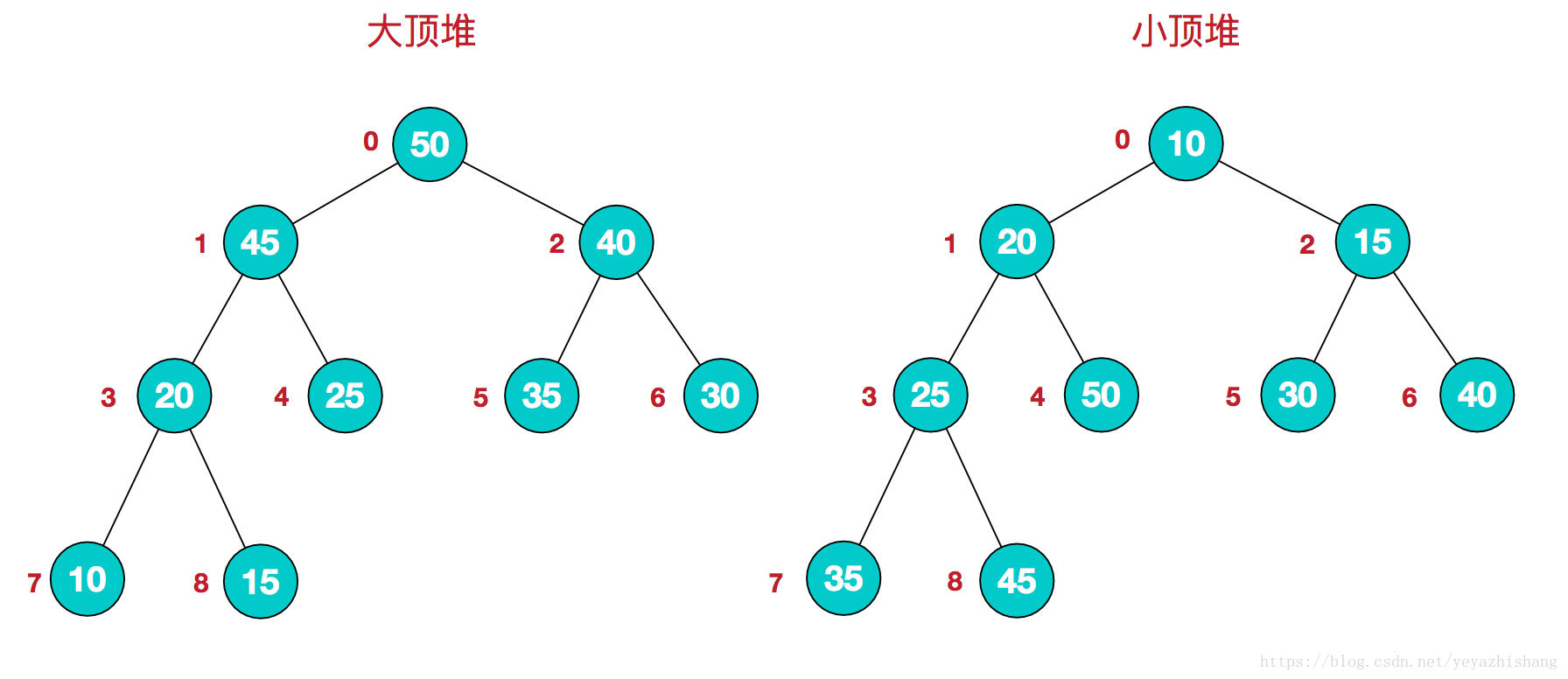
堆
- 介绍:
堆的定义如下:n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时,称之为堆
- 比较特殊的数据结构,可以被看做一棵树的数组对象
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一棵完全二叉树
- 根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等
- 满足(ki <= k2i,ki <= k2i+1)称为小顶堆
- 满足(ki >= k2i,ki >= k2i+1)称为大顶堆
散列表
- 介绍:
散列表,也叫哈希表,是根据关键码和值 (key和value) 直接进行访问的数据结构,通过key和value来映射到集合中的一个位置,这样就可以很快找到集合中的对应元素。
记录的存储位置=f(key)
这里的对应关系 f 成为散列函数,又称为哈希 (hash函数),而散列表就是把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字,然后就将该数字对数组长度进行取余,取余结果就当作数组的下标,将value存储在以该数字为下标的数组空间里,这种存储空间可以充分利用数组的查找优势来查找元素,所以查找的速度很快。
哈希表在应用中也是比较常见的,就如Java中有些集合类就是借鉴了哈希原理构造的,例如HashMap,HashTable等,利用hash表的优势,对于集合的查找元素时非常方便的,然而,因为哈希表是基于数组衍生的数据结构,在添加删除元素方面是比较慢的,所以很多时候需要用到一种数组链表来做,也就是拉链法。拉链法是数组结合链表的一种结构,较早前的hashMap底层的存储就是采用这种结构,直到jdk1.8之后才换成了数组加红黑树的结构,其示例图如下: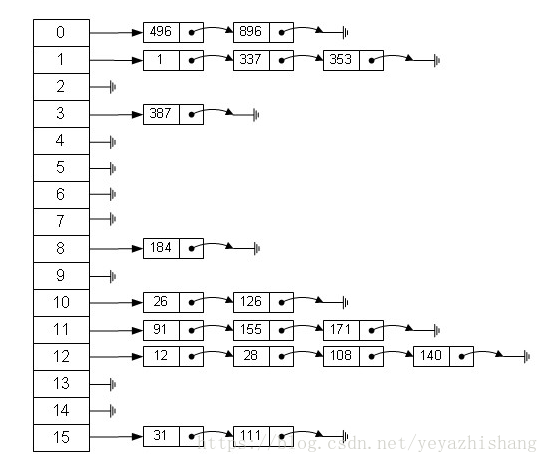
从图中可以看出,左边很明显是个数组,数组的每个成员包括一个指针,指向一个链表的头,当然这个链表可能为空,也可能元素很多。我们根据元素的一些特征把元素分配到不同的链表中去,也是根据这些特征,找到正确的链表,再从链表中找出这个元素。
哈希表的应用场景很多,当然也有很多问题要考虑,比如哈希冲突的问题,如果处理的不好会浪费大量的时间,导致应用崩溃。 - 优点:
- 查找速度快
缺点:
适用场景:
学习书籍推荐